• 목록

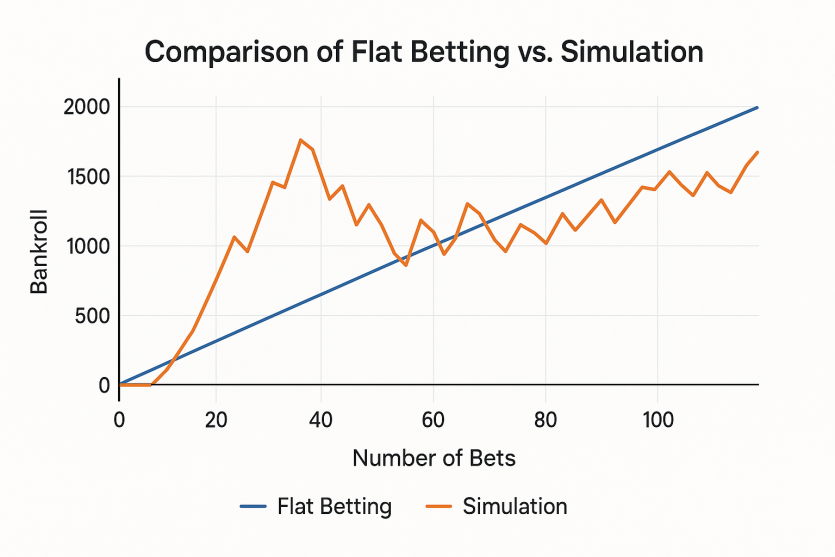
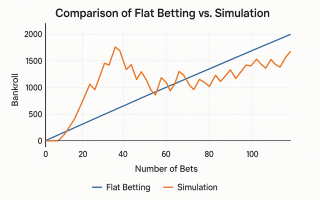
같은 확률과 같은 오즈 환경에서 피나클 정액 베팅 시뮬레이션 비교를 수행하면, 정액 플랫 스테이킹이 퍼센티지 베팅, 켈리, 하프 켈리 같은 다른 스테이킹 방식과 성능, 변동성, 리스크 면에서 어떤 차이를 보이는지 명확하게 확인할 수 있습니다.

특히 피나클 특유의 저마진 환경에서는 -105에서 -108 사이의 가격이 자주 관측되므로, 디시멀 오즈로는 대략 1.925에서 1.952 사이에 해당하는 현실적인 입력을 사용해 비교하는 것이 실전 감각과도 잘 맞습니다. 실시간 시장 데이터 대신, 확률 p의 참값을 가정해 독립 시행으로 수익을 샘플링하는 몬테카를로 구조만으로도 스테이킹별 수익 분포와 낙폭, 파산 확률의 상대적 차이를 충분히 드러낼 수 있습니다.

아래에서는 원문 핵심을 보존하면서 파라미터 설계, 위험 지표, 수치 예시, 코드, 그리고 실전 체크리스트와 FAQ를 단계적으로 보강하였으며, 여기에 바카라와 캄보디아 카지노 사례를 추가해 스포츠베팅과 카지노 게임의 시뮬레이션 방법론이 어떻게 유사·차별화되는지도 비교하였습니다.

시뮬레이션 설계 핵심

모든 단위는 디시멀 오즈 기준으로 통일해 계산 혼선을 줄입니다. 예를 들어 -105는 디시멀 1.9524로 대응하며, 베팅 1유닛을 걸었을 때 적중하면 순이익은 b = o − 1이 되고, 실패하면 −1의 손익이 발생하는 단순하고 투명한 모델을 사용합니다. 각 베팅은 확률 p로 적중한다고 가정하고, 시행 간 독립을 기본으로 하되, 실전에서는 같은 날 같은 리그의 추천들이 동조적으로 움직일 수 있으므로 상관 구조를 주입하는 옵션을 추가합니다.

비교할 스테이킹은 플랫(항상 1유닛), 퍼센티지(은행의 α%), 켈리, 하프 켈리를 기본으로 하고, 실전성을 높이기 위해 최소 스테이크·최대 스테이크 캡, 베팅 중단 임계치 등을 설정합니다.

 평가 지표로는 총손익, ROI, 최대낙폭(MDD), 파산 확률, 평균 로그 성장률을 기록해, 피나클 정액 베팅 시뮬레이션 비교에서 각 방식의 생존성과 수익성을 한눈에 볼 수 있게 합니다.

피나클형 기본 시나리오

피나클 사이드의 대표적 가격대인 -105를 반올림하여 디시멀 오즈 1.95, 즉 b = 0.95로 가정합니다. 진짜 승률 p를 0.50, 0.52, 0.55로 설정하고 EV = p·o − 1을 계산하면 무엣지, 소엣지, 중엣지 환경을 재현할 수 있습니다. 켈리 비중은 소엣지 p=0.52에서 약 1.47%로 작게 나오며, 하프 켈리는 약 0.74%입니다.

 초기 은행이 100유닛일 때 플랫 1유닛은 하프 켈리와 유사한 공격성을 보여 평균 수익이 비슷하게 움직이지만, 피나클 정액 베팅 시뮬레이션 비교를 해보면 변동성이나 최대낙폭에서 세부 차이가 드러납니다.

카지노 게임 시뮬레이션 확장 – 바카라와 캄보디아 카지노

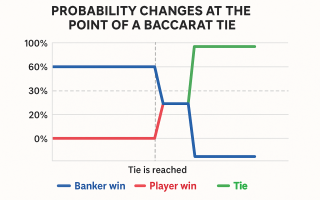
스포츠베팅과 달리 바카라 같은 카지노 게임은 확률과 배당이 고정되어 있습니다. 예를 들어 바카라에서 ‘플레이어’에 베팅할 경우 승률은 약 44.62%, 배당은 1:1, ‘뱅커’는 약 45.85%의 승률과 5% 커미션이 부과됩니다.

 이 환경에서 정액, 퍼센티지, 켈리 스테이킹을 적용한 시뮬레이션을 돌려보면, 장기 EV가 음수라는 점에서 어떤 스테이킹을 써도 손실 방향은 바뀌지 않지만, 변동성과 생존 기간은 달라집니다.

캄보디아 카지노의 바카라 테이블은 현금 칩 단위가 다양하고, 일부 VIP 룸에서는 테이블 한도를 높게 설정하기 때문에 플랫보다는 퍼센티지형이 더 자연스럽게 적용될 수 있습니다.

그러나 하우스 엣지가 존재하는 게임에서는 켈리 기준이 무의미해지고, 오히려 플랫이나 보수적인 퍼센티지 스테이킹으로 손실 속도를 늦추는 것이 유리합니다.

이 역시 피나클 정액 베팅 시뮬레이션 비교에서 얻은 인사이트와 연결되는데, EV가 음수일 때 스테이킹은 단지 ‘얼마나 천천히 질 것인가’를 결정하는 도구라는 점이 동일합니다.

손계산 예시와 코드, 그리고 실전 체크리스트

1. 손계산으로 보는 정액의 변동성 감
소엣지 시나리오에서 플랫 1유닛 기준 1회 기대값은

????=????⋅????−(1−????)μ=p⋅b−(1−p)여기서 ????=0.52p=0.52, ????=0.95b=0.95이므로

????=0.52×0.95−0.48=0.494−0.48=0.014
μ=0.52×0.95−0.48=0.494−0.48=0.014

분산 계산:

????−????=0.95−0.014=0.936,(0.936)2=0.876096,0.52×0.876096
≈0.45557b−μ=0.95−0.014=0.936,(0.936)
2=0.876096,0.52×0.876096≈0.45557

반대 항:

−1−????=−1.014,(−1.014)2=1.028196,0.48×
1.028196≈0.49353−1−μ=−1.014,(−1.014)
2 =1.028196,0.48×1.028196≈0.49353

따라서 분산:

Var≈0.45557+0.49353=0.94910Var≈0.45557+0.49353=0.94910

표준편차:

????≈0.94910≈0.974σ≈ 0.94910≈0.974
n = 1000회라면 기대이익은 +14유닛, 표준편차는 약
0.974×1000≈30.80.974× 1000
​
 ≈30.8 유닛입니다.95% 신뢰범위는 14±1.96×30.8
14±1.96×30.8, 즉 대략 -47.6 ~ +75.6 유닛에 걸쳐 분포합니다.

이 범위는 실전에서 장기 손실 구간을 경험할 확률이 높다는 것을 의미합니다.

2. 파이썬 시뮬레이션 예제

python
복사
편집
import random, math
from statistics import mean

def run_sim(n_bets=1000, bankroll0=100.0, odds=1.95, p_true=0.52,
staking='flat',
flat_unit=1.0, pct=0.01,
kelly_cap=0.05, # 켈리 최대치
stake_min=0.0,
stake_max=None,
ruin_floor=10.0,
stop_drawdown=None,
rho=0.0):

b = odds - 1.0
bk = bankroll0
peak = bankroll0
mdd = 0.0
ruined = False
logs = []
staked_sum = 0.0

for _ in range(n_bets):
 # 스테이크 결정
if staking == 'flat':
stake = flat_unit
elif staking == 'percent':
stake = bk * pct
elif staking in ('kelly', 'half_kelly'):
f_star = ((b * p_true) - (1 - p_true)) / b
f_star = max(0.0, min(f_star, 1.0))
if staking == 'half_kelly':
f_star *= 0.5
f_star = min(f_star, kelly_cap)
stake = bk * f_star

 else:
raise ValueError("Unsupported staking type")

# 최소·최대 스테이크 적용
if stake_max is not None:
 stake = min(stake, stake_max)
if stake_min is not None:
stake = max(stake, stake_min)

stake = min(stake, bk)  # 자금 부족 방지
if stake <= 0 or bk <= 0:
ruined = True
break

staked_sum += stake

# 공통 충격 상관 반영
 z = random.random()
if z < rho:
win = 1 if random.random() < p_true else 0

3. 실전 체크리스트

평균 오즈와 p의 보수적 추정치를 명확히 설정하고, CLV로 정기 검증하고 있는가?

초기 은행 대비 플랫 1유닛이 0.5~1.0% 범위에 들어가는가?

퍼센티지 α와 켈리 캡이 지나치게 공격적이지 않은가?

**최대 허용 낙폭(MDD)**과 파산 플로어를 사전에 수치로 정의했는가?

같은 날 베팅 상관(rho)을 고려해 총 익스포저 상한을 운영하는가?

기록 체계를 표준화해 p5, p50, p95, MDD, ruin을 주기적으로 점검하는가?

엣지 추정이 변하면 즉시 스테이킹을 재조정하는 규칙이 있는가?

이렇게 하면

손계산 → 이론적으로 변동성을 직관적으로 이해

코드 → 실제 시뮬레이션 구현 가능

체크리스트 → 실전 운영 규칙 수립 가능

원하시면 여기에 바카라와 캄보디아 카지노 시뮬레이션 코드 버전**도 추가해서, 스포츠베팅·카지노 환경을 통합 비교할 수 있게 만들어 드릴 수 있습니다.

그걸 넣으면 피나클 분석과 카지노 분석을 하나의 프레임워크에서 다룰 수 있게 됩니다.

FAQ

Q1. p(승률) 추정이 시간에 따라 변하면 스테이킹을 어떻게 조정해야 하나요?

A1. 베팅마다 동적으로 p를 재추정하고, 켈리 비율을 갱신하되, 켈리 캡과 최소 스테이크를 동시에 설정해야 합니다. p 변동성이 클수록 하프·쿼터 켈리를 권장하고, 불확실 구간에서는 플랫으로 다운시프트하는 것이 안전합니다.

Q2. 장기 베팅 횟수(n)가 적으면 퍼센티지나 켈리가 불리하지 않나요?

A2. n이 작으면 분산이 커져 꼬리 리스크가 커집니다. 초기에는 플랫+하프 켈리 혼합이 현실적이고, CLV와 실현 수익률이 안정화되는 것이 확인되면 점진적으로 공격성을 높이는 것이 좋습니다.

Q3. 바카라나 캄보디아 카지노에서도 켈리 전략이 유효한가요?

A3. 하우스 엣지가 존재하는 게임(예: 바카라)은 장기 EV가 음수이므로 켈리 최적화의 의미가 없습니다. 오히려 손실 속도를 늦추기 위해 플랫 또는 소액 퍼센티지 스테이킹을 사용하는 것이 유리합니다.

Q4. 롱샷(고배당) 중심 전략에서는 스테이킹을 어떻게 설정하나요?

A4. 오즈가 커질수록 분산이 커지므로 α(퍼센티지)나 f*(켈리)를 더 낮게 설정해야 합니다. 오즈 구간별로 다른 α를 쓰거나, 로그 성장률 기준으로 최적 f를 재산정하는 방식이 안전합니다.

Q5. 파산 플로어는 어느 수준으로 설정하는 게 좋나요?

A5. 심리적·재정적 한계를 반영합니다. 일반적으로 초기 은행의 10~20% 구간을 플로어로 두고, 도달 시 자동 중단·모델 점검·스테이킹 축소를 트리거하는 규칙이 좋습니다.

Q6. CLV(Closing Line Value)가 플러스인데 손실이 나는 경우는 왜 그런가요?

A6. 단기 표본 잡음일 가능성이 높습니다. 장기적으로는 EV에 수렴할 확률이 높지만, 특정 리그·시장에 한정된 괴리가 지속된다면 p 추정 바이어스나 표본 선택 문제를 점검해야 합니다.

Q7. 하프 켈리와 플랫 중 어느 쪽이 더 좋은가요?

A7. p 추정이 안정적이고 n이 충분하면 하프 켈리가 로그 성장률 측면에서 우세합니다. 반대로 불확실성이 높거나 상관이 크면 플랫이 생존성 측면에서 유리합니다.

Q8. 퍼센티지 베팅의 α는 어떻게 정하나요?

A8. 은행의 0.5~1.0%로 시작해, p 안정성·CLV·낙폭 경험을 바탕으로 서서히 조정합니다. 지나치게 높은 α는 변동성을 과도하게 키워 파산 확률을 높입니다.

Q9. 피나클 정액 베팅 시뮬레이션 비교 결과를 카지노에도 적용할 수 있나요?

A9. 가능합니다. 특히 변동성, 최대낙폭, 생존 기간 분석은 카지노 게임에도 그대로 적용됩니다. 단, EV가 음수인 게임에서는 수익 극대화보다는 손실 속도 완화가 목표가 됩니다.

Q10. 같은 날 다수 베팅의 상관성은 어떻게 처리하나요?

A10. 시뮬레이션에 **rho(상관 계수)**를 주입하거나, 동일 시간대 베팅을 묶어 총 익스포저 상한을 설정합니다. 상관이 높아질수록 최대낙폭과 꼬리 리스크가 커집니다.

#온라인카지노#스포츠토토#바카라명언 #바카라사이트주소 #파워볼사이트 #카지노슬롯머신전략 #카지노게임 #바카라사이트추천 #카지노사이트주소 #온라인카지노가이드 #카지노게임추천 #캄보디아카지노 #카지노게임종류 #온라인슬롯머신가이드 #바카라성공 #텍사스홀덤사이트 #슬롯머신확률 #마닐라카지노순위 #바카라금액조절 #룰렛베팅테이블 #바카라배팅포지션